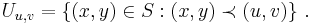Lexicographic order topology on the unit square

In mathematics, and especially general topology, the lexicographic ordering on the unit square is an example of a topology on the unit square S, i.e. on the set of points (x,y) in the plane such that 0 ≤ x ≤ 1 and 0 ≤ y ≤ 1.[1] To give S a topology means to say which subsets of S are "open", and to do so in a way that the following axioms are met:[2]

  1. The union of open sets is an open set.
  2. The finite intersection of open sets is an open set.
  3. S and the empty set ∅ are open sets.

This is an example of an order topology in which there are uncountably many pairwise disjoint homeomorphic copies of the real line.

Construction

As the name suggests, we use the lexicographical ordering on the square to define a topology. Given two points in the square, say (x,y) and (u,v), we say that (x,y) \scriptstyle\prec (u,v) if and only if either x < u or both x = u and y < v. Given the lexicographical ordering on the square, we use the order topology to define the topology on S.[1] For each point (u,v) we get an open set, denoted Uu,v, given by all the points in S that precede (u,v) with respect to the lexicographical ordering:

U_{u,v} = \{ (x,y) \in S�: (x,y) \prec (u,v) \} \ .

The open sets in the lexicographic ordering on the unit square are the whole set S, the empty set ∅, and those sets generated by the Uu,v, i.e. the sets formed by all possible unions of finite intersections.[3]

See also

References

  1. ^ a b Steen, L. A.; Seebach, J. A. (1995), Counterexamples in Topology, Dover, p. 73, ISBN 048668735X 
  2. ^ Steen, L. A.; Seebach, J. A. (1995), Counterexamples in Topology, Dover, p. 3, ISBN 048668735X 
  3. ^ Steen, L. A.; Seebach, J. A. (1995), Counterexamples in Topology, Dover, p. 4, ISBN 048668735X